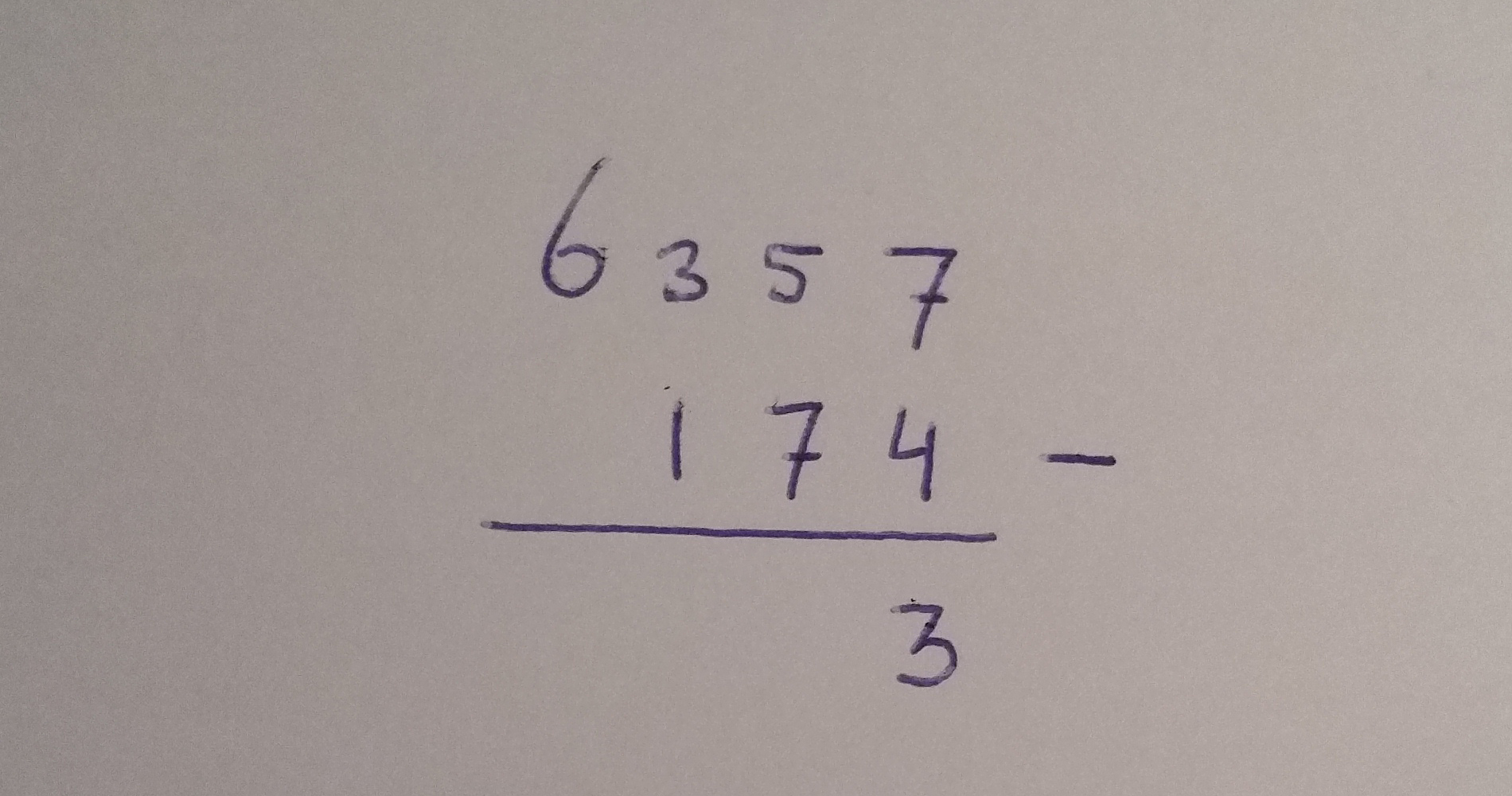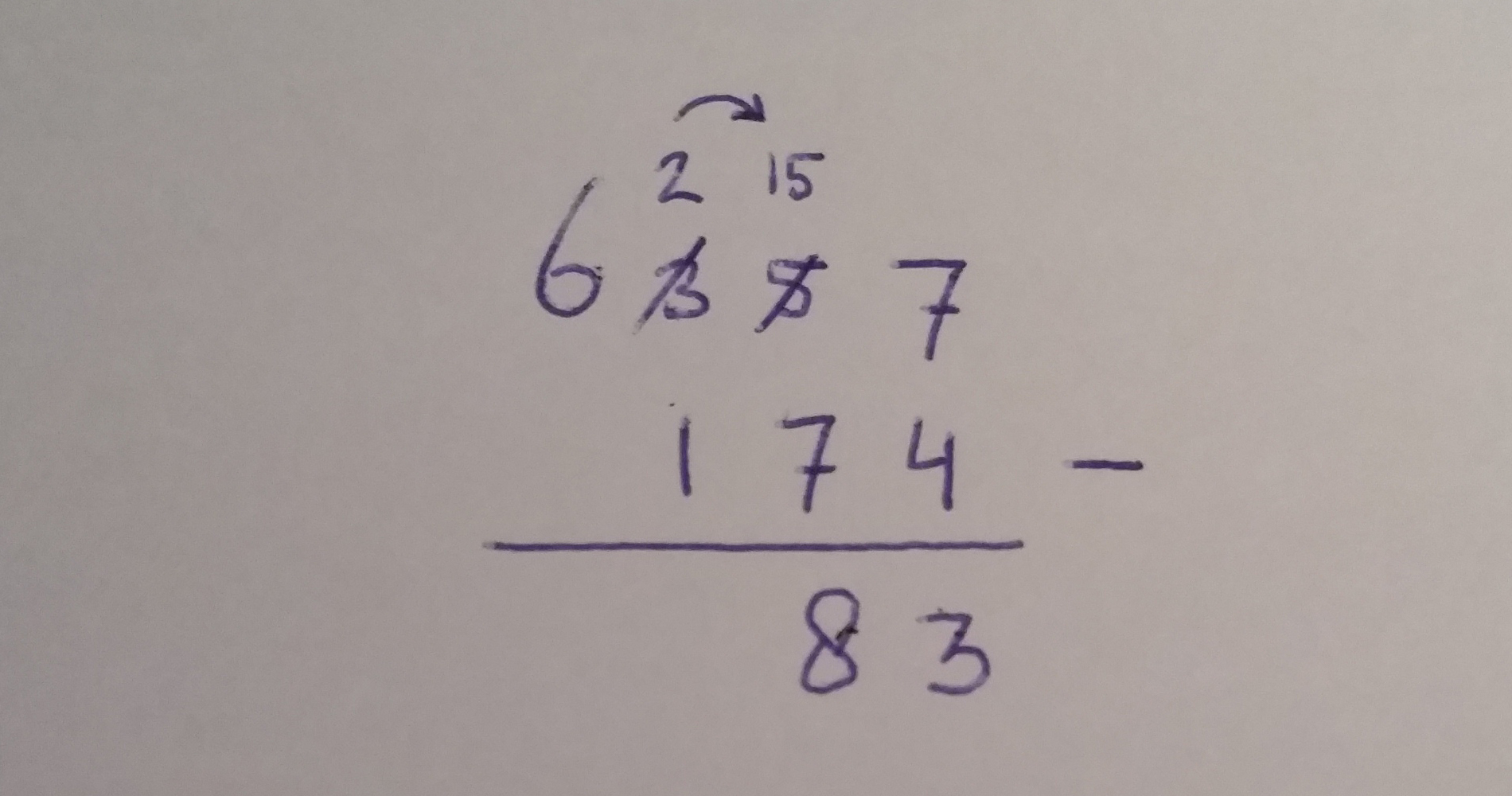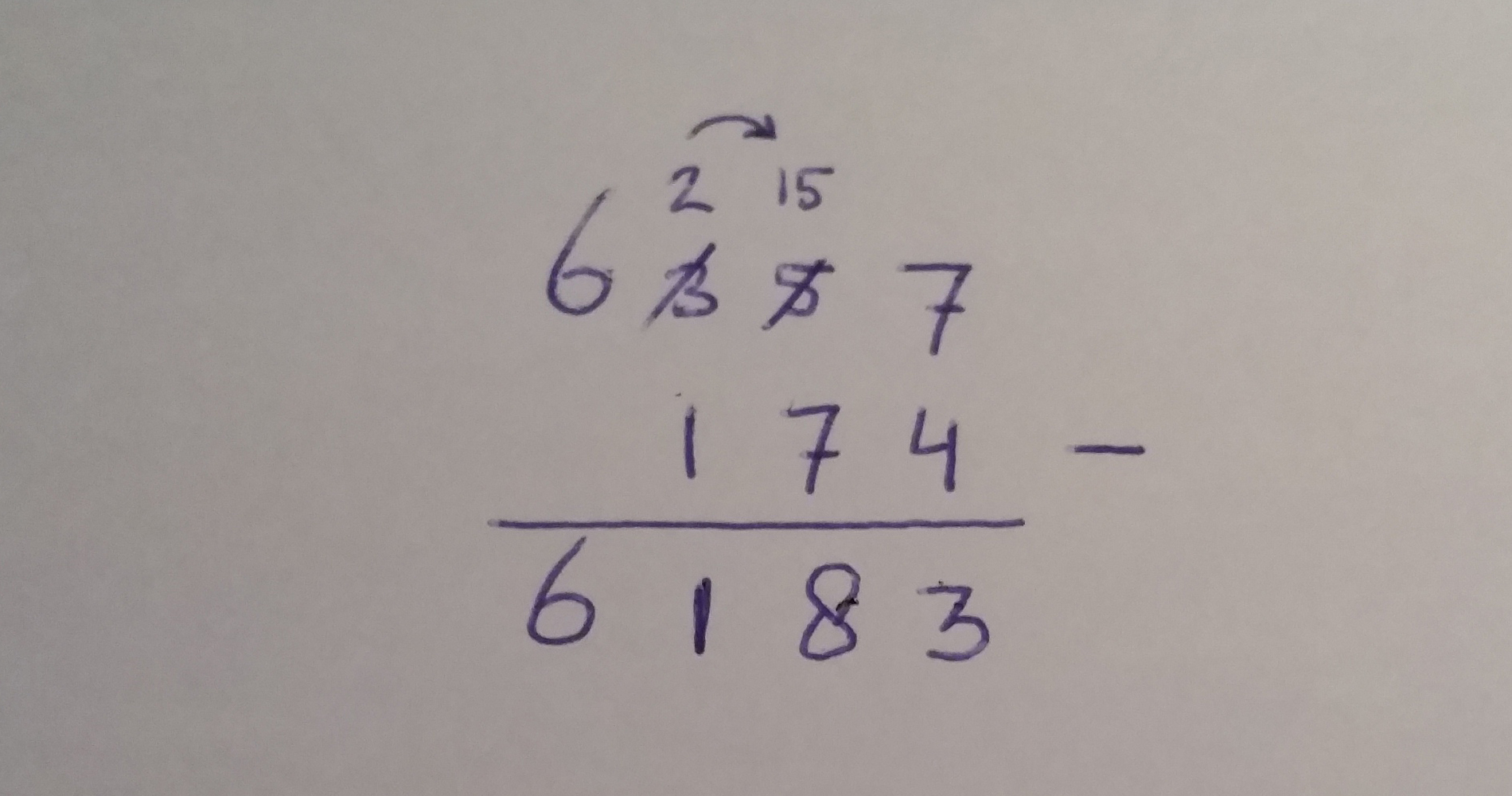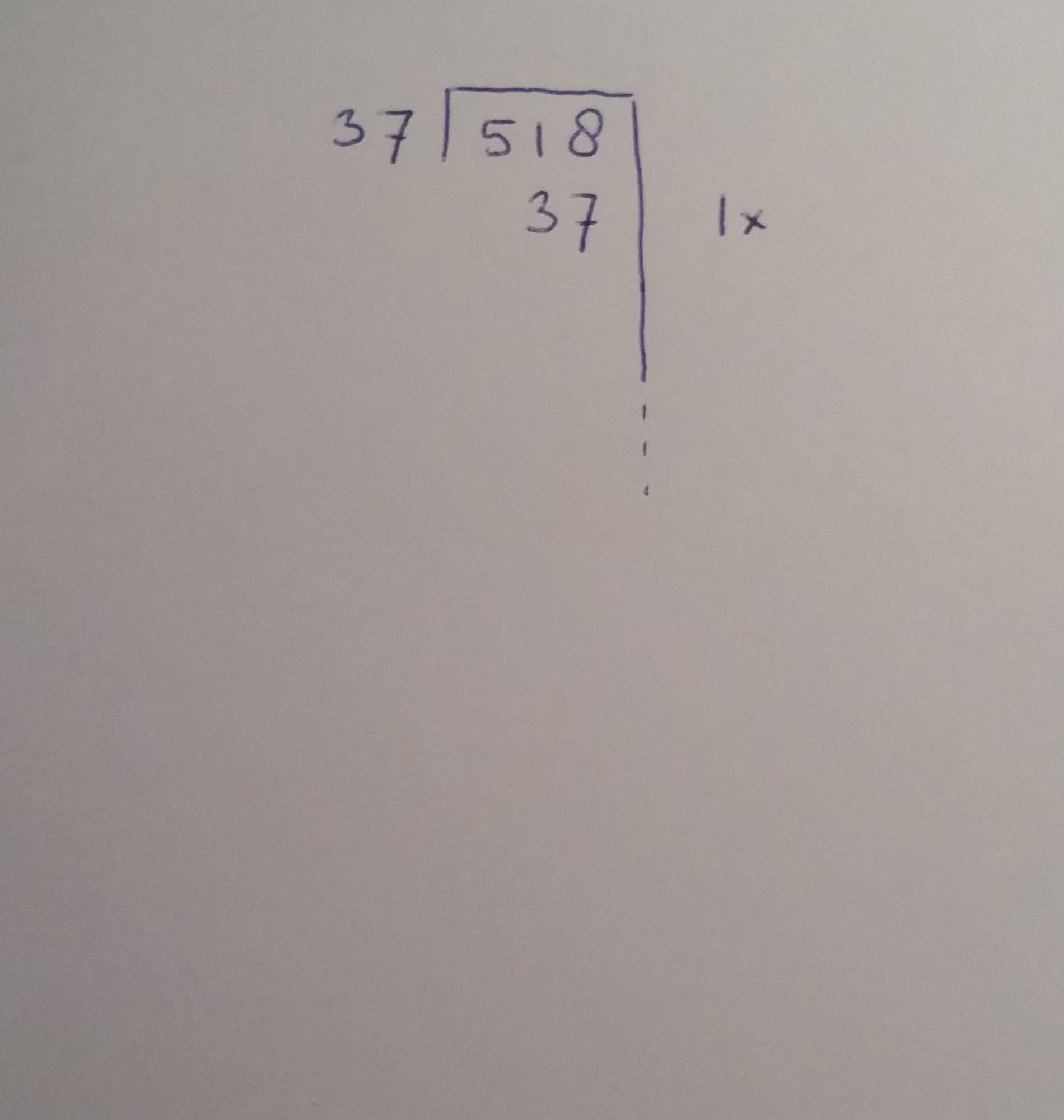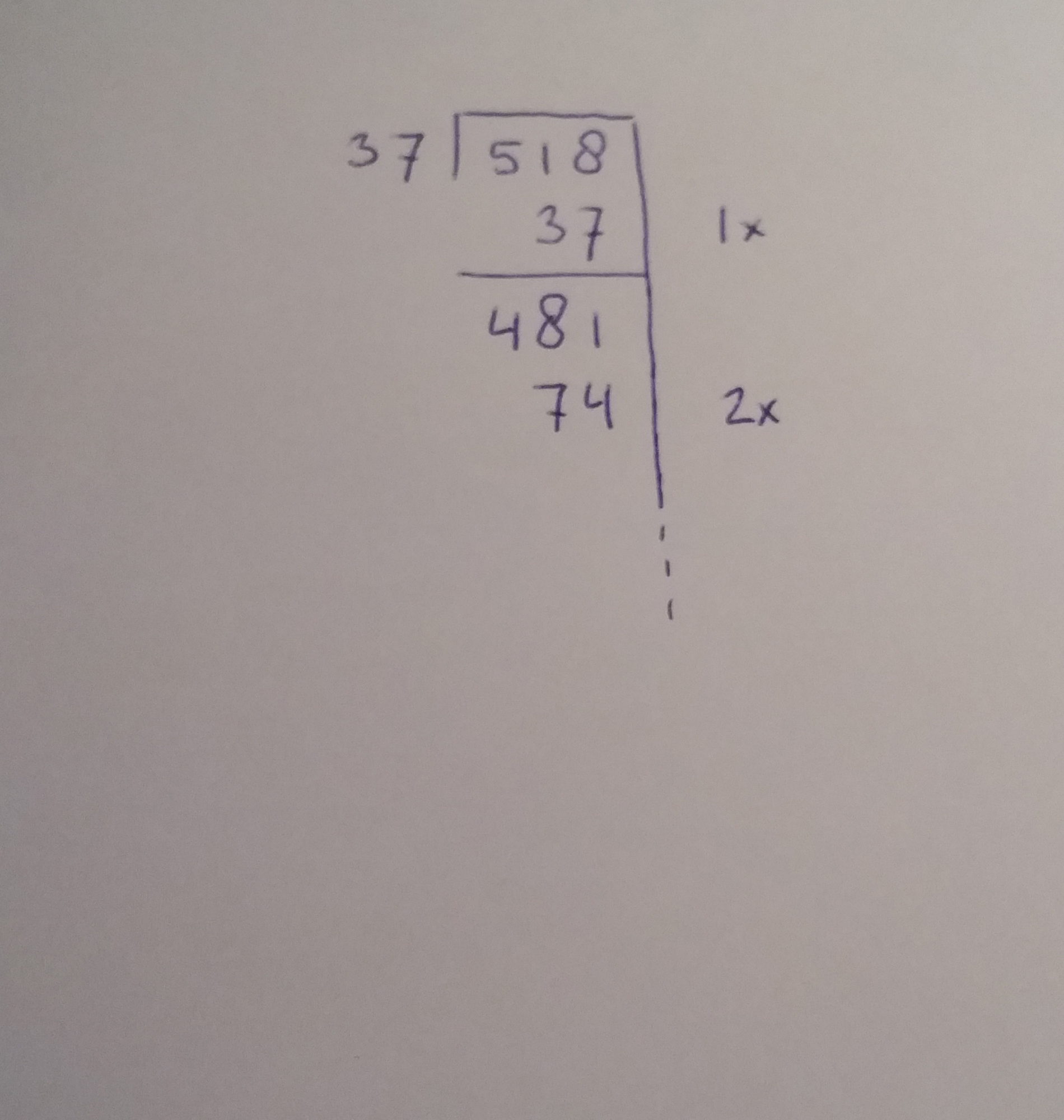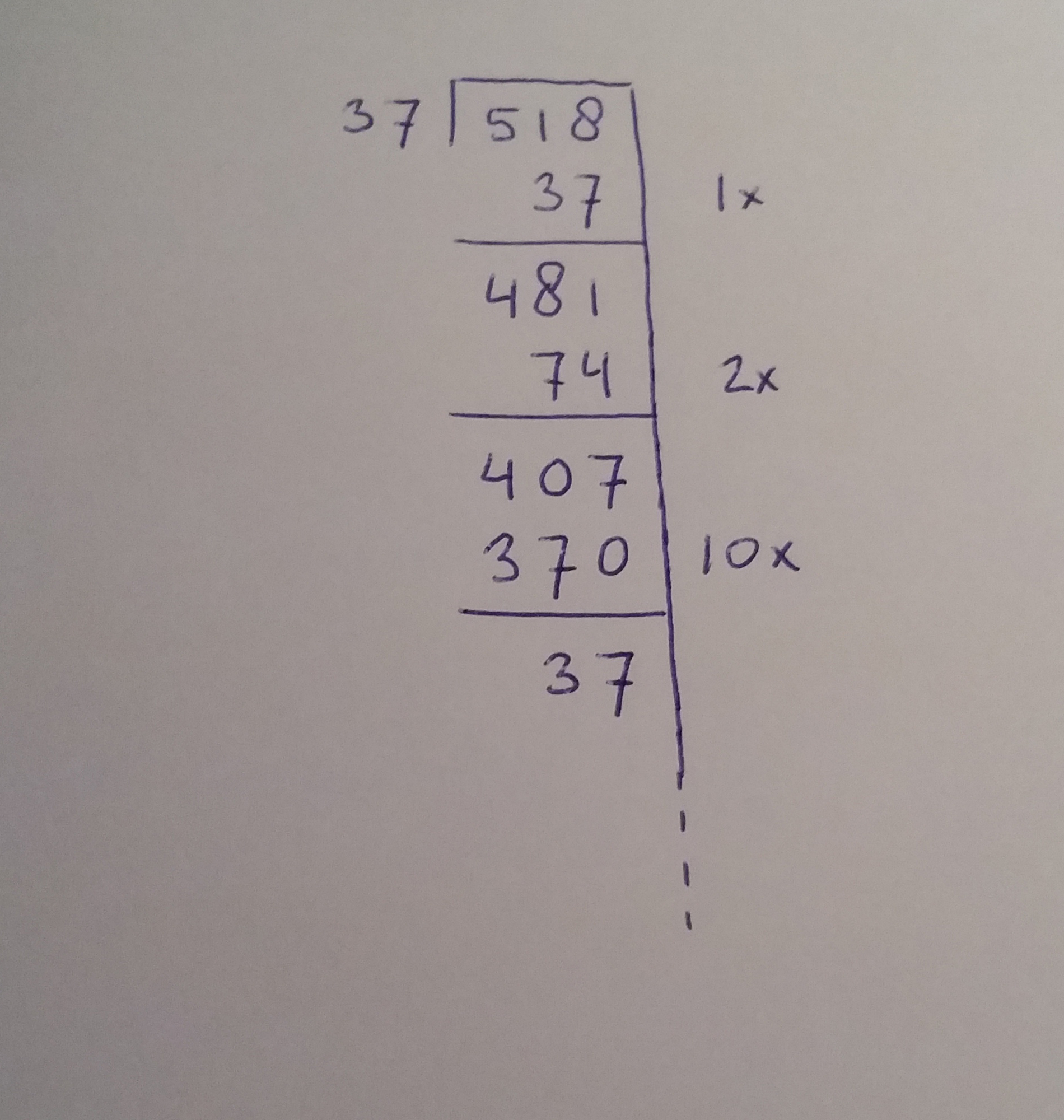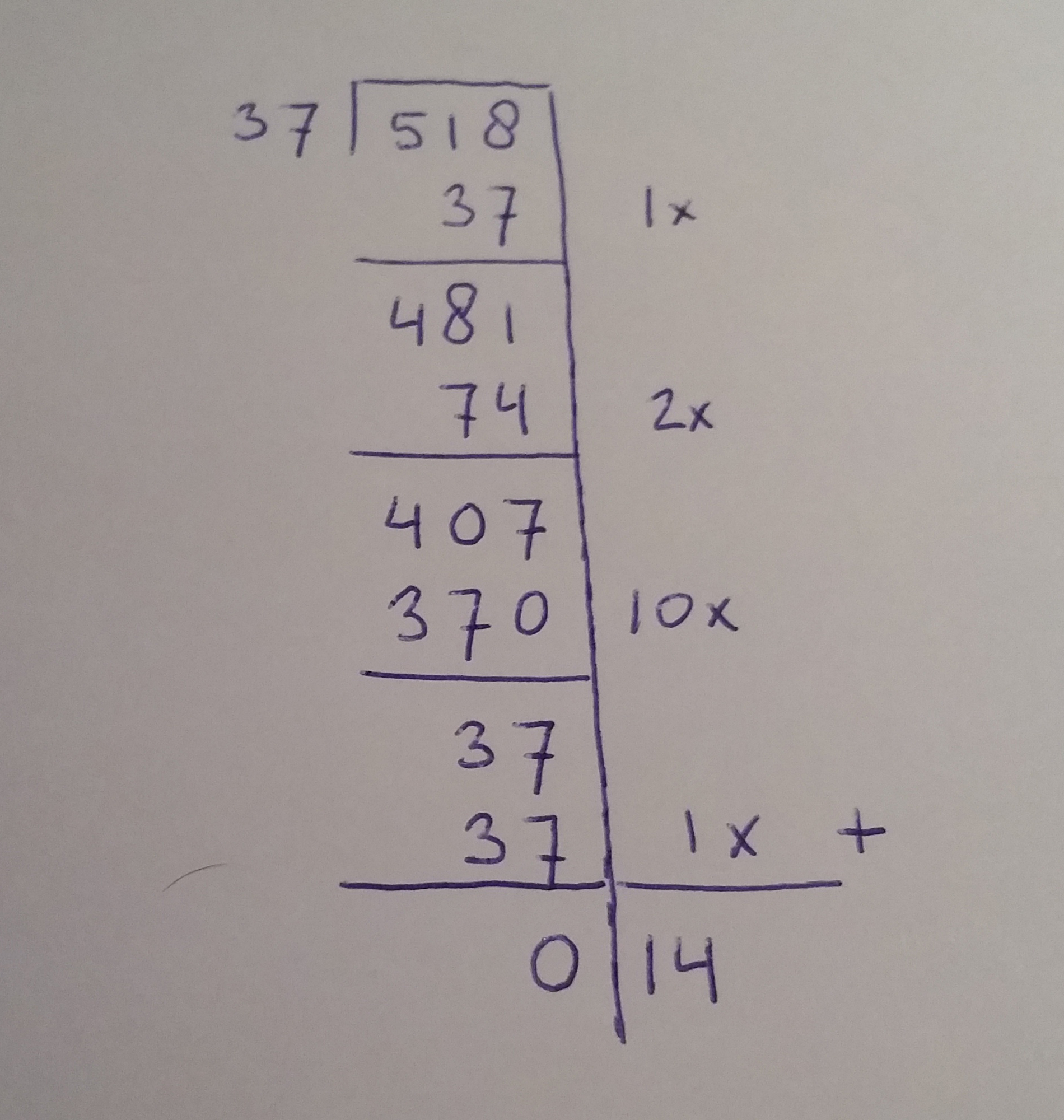Op dit gedeelte van de site staan de eerste zetten richting een systeem dat leerlingen de kans biedt om zelf te zoeken naar oplossingsstrategieën voor rekenkundige problemen.
Noem het Remedial Teaching, noem het bijles, maar bovenal wil ik de leerling in staat stellen om buiten werkelijke bijlessen om toch verder te kunnen komen met te maken sommen.
En dat alles liefst eenvoudig toegankelijk op de mobiele telefoon (of op zijn minst een laptop).
Nu eens zien of een klupje docenten er mee uit de voeten kan…
Succes, LC-ers!
Voorbeeld uitleg (heftig onderhevig aan uitbouw en aanpassingen)
Cijferend aftrekken
Bijvoorbeeld 6357 – 174 =
- Schrijf de getallen onder elkaar
- Houd rekening met eenheden, tientallen, etc.
Stap 1: eenheden aftrekken
- 7 – 4 = 3
Stap 2: tientallen aftrekken
- 5 tientallen is te weinig, dus wisselen
- 1 honderdtal wisselen voor 10 extra tientallen
- 15 – 7 = 8
Stap 3: hondertallen / duizendtallen aftrekken
- 2 – 1 = 1
- 6 – 0 = 6
Cijferend delen (de haakdeling)
Bijvoorbeeld 518 : 37 =
- Lees: ‘hoe vaak past 37 in 518’
- Zet de getallen als onderstaand in een ‘haak’
Stap 1: voorzichtige eerste stapjes
- 37 past zeker 1x in 518; noteer als volgt
Stap 2: restant berekenen en volgende stap
- 518 – 37 = 481
- De volgende stap nemen we iets groter; 37 past ook wel 2x in 481
Stap 3: restant berekenen en volgende stap
- 481 – 74 = 407
- De volgende stap kan nog groter; 10x ineens eraf
- 407 – 370 = 37
Stap 4: een laatste stap, en resultaat berekenen
- Met een restant van 37 past 37 nog maar 1x
- 37 – 37 = 0
- Aan de rechterkant van de ‘haak’ staat steeds hoe vaak we 37 van het restant af hebben gehaald; dit tellen we bij elkaar op
Het antwoord van de som staat nu aan de rechterkant onder de streep:
518 : 37 = 14
Tips: de eerste stap hoeft niet per se klein te zijn, je kunt ook meteen groter beginnen – hoe groter de stappen, hoe korter de som.