Leerlingen.

Je kunt niet met ze, en je kunt niet zonder ze. Vrij letterlijk zelfs, dat laatste. Want klassen zonder leerlingen leiden vrij snel (denk ik) tot het einde van mijn loopbaan in het onderwijs.

Maar zo af en toe komen ze met pareltjes van opmerkingen. Daar houd ik van.

Zoals bijvoorbeeld het volgende. In ons rekenboek (van een niet nader genoemde methode van een niet nader genoemde uitgever) staat de volgende som:

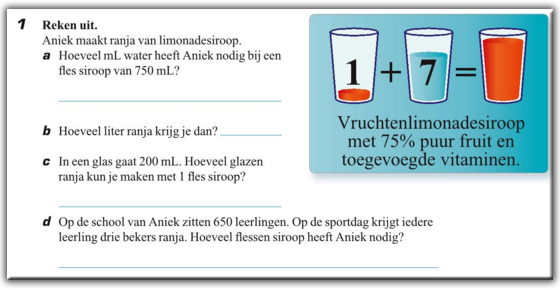
We behandelen de som in de les, bedenken klassikaal wat de antwoorden op de vragen zijn en leerlingen leggen uit hoe ze op hun antwoord zijn gekomen.

En dan komen we bij vraag (d). En merkt een leerling op: “Meneer, vraag (d) kunnen we niet oplossen, want ze vertellen er niet bij hoeveel ranja er in een beker past.”

Ik kijk even goed, en begin aan een zin waarin ik uit wil leggen dat er toch heel duidelijk bij vraag (c) vermeld staat hoeveel er in een… juist ja, ‘glas’ zit. Dus niet ‘beker’. Dus ik stop met praten, want ik zie het ‘probleem’.

En als ik even eerlijk mag zijn (en dat mag ik), dan geef ik deze leerling gelijk. Om de continuïteit te bewaren had ik er zelf voor gekozen om het in de gehele som over OF glazen, OF bekers te hebben. Ik heb me nog even afgevraagd of de uitgever het misschien expres heeft gedaan. Maar eigenlijk denk ik van niet. Ik vind het slordig.

Je kunt er wat van vinden (kan ik ook: even logisch nadenken en je begrijp toch wel dat ze er hetzelfde mee bedoelen!), maar even heel droog bekeken: de leerling heeft gelijk. Een beker is niet hetzelfde als een glas. Bedenk ik wat voor glazen ik thuis heb staan, en hoe een beker die doorgaans op sportdagen wordt uitgedeeld er uit ziet, dan wijkt de inhoud waarschijnlijk af.

En op sportdagen geef je mensen niet drie keer een glas ranja. Dat doe je in (plastic/kartonnen) bekers. En er staat nergens in de som hoeveel er in zo’n beker past.

Een slechte som is het niet (leuk om klassikaal op te lossen), maar de uitgever krijgt toch even een mailtje. Of ze het woord ‘ranja’ alsjeblieft willen vervangen door ‘limonade’.

Leerlingen, bedankt!

Het sportprogramma Bureau Sport laat bekende Nederlanders een race over 100 meter schaatsen tegen oud-wereldkampioen sprint Jeremy Wotherspoon.

Wotherspoon klokt na 100 meter 9,60 seconden. De bekende Nederlander klokt 13,41 seconden over diezelfde 100 meter.

Hoeveel meter ligt de bekende Nederlander achter na 100 meter? Rond af op hele meters.

Dit vraagstuk staat in één van de afgelopen 3F examens (MBO niveau 4), en ik heb ‘m geselecteerd op een korte ’toets’ om te zien hoe leerlingen om gaan met dit soort examenvragen.

Ik kom er dan toch weer achter hoe belangrijk het is hoe een vraag is verwoord. Ik was van tevoren namelijk al van mening dat de manier waarop de vraag is gesteld, open staat voor interpretatie.

Blijkbaar had ik gelijk, want ik zie een drietal antwoorden met grote regelmaat voorbij komen (0 meter, 28 meter en 40 meter).

En ik vind voor alle drie wat te zeggen. En dat vind ik dus niet goed.

Ruimte voor interpretatie hoort niet op een examen som. Daar kun je wat van vinden, maar persoonlijk vind ik nog steeds dat we rekenvaardigheid moeten toetsen, en niet leesvaardigheid.

Ik heb leerlingen gevraagd mij te vertellen hoe ze aan hun antwoorden zijn gekomen. Het volgende kwam naar boven:

Bij het antwoord ‘0 meter’ beredeneren leerlingen dat, wanneer de bekende Nederlander over de streep komt na 13,41 seconden, Jeremy Wotherspoon daar op ‘m staat te wachten, en dan zijn ze dus allebei 100 meter ver, en is er geen verschil meer. Klinkt raar? Ik vond het best slim bedacht (verplaats je ook even in de gedachten van mijn niveau 4 MBO leerlingen, mocht je het echt klinkklare onzin vinden…).

Bij het antwoord ’40 meter’ bedenken leerlingen dat Jeremy Wotherspoon op volle snelheid door schaatst na het passeren van de 100 meter lijn (en dus 13,41 – 9,6 = 3,81 seconden lang zijn gemiddelde snelheid blijft rijden).

En bij het (correcte) antwoord ’28 meter’ berekenen ze op het moment dat Wotherspoon de 100 meter lijn passeert, hoe ver de bekende Nederlander is.

Dat is overigens 100 : 13,41 ( = de gemiddelde snelheid van de bekende Nederlander) x 9,6 seconden (de tijd waarop de wedstrijd in principe over is, omdat Wotherspoon dan finisht). In de meeste gevallen halen de leerlingen dan deze afstand af van de 100 meter (en genoeg anderen vergeten dat er gevraagd is hoeveel meter de bekende Nederlander achter loopt).

Mijn voorstel: verwoord de vraag anders.

Hoeveel meter ligt de bekende Nederlander achter op het moment dat Jeremy Wotherspoon 100 meter heeft geschaatst?

Zie er op toe dat de rekenexamens een directe uitwerking zijn van uw beleidsinzet: de rekenvaardigheid op een hoger plan brengen. En zorg ervoor dat de examens niet het begrijpend lezen meten, omdat zij te talig zijn.

Één van de discussiepunten over de huidige rekenexamens is de ’taligheid’ er van. Het is een discussie omdat leerlingen die de examens moeten maken (samen met de docenten die ze op de betreffende examens moeten voorbereiden) vinden dat het soms nodeloos ingewikkeld is om de juiste informatie uit de begeleidende tekst bij een som te halen, en de makers van de examens (en de examensommen individueel) uiteraard vinden dat het zo prima is. Ik zeg daarbij ‘uiteraard’, omdat ik het natuurlijk ook niet leuk zou vinden om te horen dat een door mij bedachte som niet geschikt wordt geacht voor een examen…

Maar het is wel goed om daar even bij stil te staan. Wat willen we toetsen met de rekenexamens? Pure rekenvaardigheid? Of toch ook het vermogen om informatie te filteren, te onderscheiden wat belangrijk is om een som te kunnen berekenen?

Hier zou je het lang over kunnen hebben natuurlijk, maar rekenen draait volgens mij om het beheersen van bepaalde rekenvaardigheden (die je later dan weer kunt gebruiken of zelfs nodig hebt bij andere vakken, zoals bijvoorbeeld wiskunde…) en oplossingsstrategieën, en kan derhalve wat mij betreft los worden gekoppeld van het kunnen filteren van informatie.

Anderzijds zou ik best overgehaald kunnen worden om toch een enkele som in het examen te stoppen waarbij wat meer taligheid komt kijken, om zo leerlingen ook een beetje beter voor te bereiden op een vak als wiskunde A (hier moet ik even toegeven dat ik de term gebruik voor een variant wiskunde zoals ik het nog kreeg om de middelbare school; mocht wiskunde A verloren zijn gegaan en tegenwoordig anders heten, dan lees ik dat vast wel terug in de reacties), maar in de huidige vorm van de examens vind ik de verhouding bijna belachelijk scheef.

Een examen 2F of 3F bestaat nu gemiddeld genomen uit zo’n 40 vragen, waarvan er tussen de 5 en 10 ‘pure’ rekensommen zijn. Deze moeten worden gemaakt met slechts hulp van een kladblaadje, en zien er uit als simpele rekenopgaven. Bij de rest van de 40 vragen mag, naast het kladblaadje, een rekenmachine worden gebruikt, en zijn het allemaal de ‘plaatje/verhaaltje/vraag’ sommen geworden.

Om het geheel te verduidelijken geef ik even een voorbeeld van een examenopgave uit een 3F examen.

Bij het uitrekenen van een gemiddelde (in dit geval dus het gemiddelde aantal inwoners per vierkante kilometer) heb ik voldoende aan twee getallen: het totaal aantal inwoners, en de totale oppervlakte in vierkante kilometers. Kwestie van even delen, en het antwoord is daar. Ik moet het hier afronden op één decimaal, wat ergens een beetje raar is omdat 0,3 inwoner natuurlijk iets is wat ik in het dagelijks leven niet vaak zal tegen komen, maar daar kan ik nog wel langs heen kijken.

Het gaat nu uiteraard meer even om de toevoegingen in de tekst. ‘Het is 11 keer zo groot als Nederland en 15 keer zo groot als België.’ Uit ervaring kan ik inmiddels vertellen dat dit soort toevoegingen dermate veel impact heeft op de lezer, dat het mijns inziens veel te veel afleidt van wat ik zelf in een som als deze getoetst wil hebben; het kunnen berekenen van een gemiddelde. ‘86% van de bevolking is Zweeds.’ En we mikken er ook nog even een percentage bij in de tekst, want dat doet het ook altijd leuk. Ik ben best in staat om deze gegevens te nemen voor wat ze zijn: afleidingsmanoeuvres, niets meer en niets minder. Maar ik kan intussen ook vertellen dat zowel mijn leerlingen als mijn collega’s zich ernstig laten afleiden en amper nog in staat zijn om het juiste antwoord op deze som te geven.

En dan vraag ik me dus af: ben ik rekenen aan het toetsen, of begrijpend lezen? Schiet zo’n opgave niet een beetje voorbij aan het doel van het rekenexamen? U mag het zeggen.

(Quote is gehaald uit een adviesbrief van het Steunpunt Taal en Rekenen MBO, aan de minister van onderwijs; de examenopgave is er één van uitgever Deviant, gevonden in een 3F oefenexamen uit de digitale leeromgeving Studiemeter.)