Zie er op toe dat de rekenexamens een directe uitwerking zijn van uw beleidsinzet: de rekenvaardigheid op een hoger plan brengen. En zorg ervoor dat de examens niet het begrijpend lezen meten, omdat zij te talig zijn.

Één van de discussiepunten over de huidige rekenexamens is de ’taligheid’ er van. Het is een discussie omdat leerlingen die de examens moeten maken (samen met de docenten die ze op de betreffende examens moeten voorbereiden) vinden dat het soms nodeloos ingewikkeld is om de juiste informatie uit de begeleidende tekst bij een som te halen, en de makers van de examens (en de examensommen individueel) uiteraard vinden dat het zo prima is. Ik zeg daarbij ‘uiteraard’, omdat ik het natuurlijk ook niet leuk zou vinden om te horen dat een door mij bedachte som niet geschikt wordt geacht voor een examen…

Maar het is wel goed om daar even bij stil te staan. Wat willen we toetsen met de rekenexamens? Pure rekenvaardigheid? Of toch ook het vermogen om informatie te filteren, te onderscheiden wat belangrijk is om een som te kunnen berekenen?

Hier zou je het lang over kunnen hebben natuurlijk, maar rekenen draait volgens mij om het beheersen van bepaalde rekenvaardigheden (die je later dan weer kunt gebruiken of zelfs nodig hebt bij andere vakken, zoals bijvoorbeeld wiskunde…) en oplossingsstrategieën, en kan derhalve wat mij betreft los worden gekoppeld van het kunnen filteren van informatie.

Anderzijds zou ik best overgehaald kunnen worden om toch een enkele som in het examen te stoppen waarbij wat meer taligheid komt kijken, om zo leerlingen ook een beetje beter voor te bereiden op een vak als wiskunde A (hier moet ik even toegeven dat ik de term gebruik voor een variant wiskunde zoals ik het nog kreeg om de middelbare school; mocht wiskunde A verloren zijn gegaan en tegenwoordig anders heten, dan lees ik dat vast wel terug in de reacties), maar in de huidige vorm van de examens vind ik de verhouding bijna belachelijk scheef.

Een examen 2F of 3F bestaat nu gemiddeld genomen uit zo’n 40 vragen, waarvan er tussen de 5 en 10 ‘pure’ rekensommen zijn. Deze moeten worden gemaakt met slechts hulp van een kladblaadje, en zien er uit als simpele rekenopgaven. Bij de rest van de 40 vragen mag, naast het kladblaadje, een rekenmachine worden gebruikt, en zijn het allemaal de ‘plaatje/verhaaltje/vraag’ sommen geworden.

Om het geheel te verduidelijken geef ik even een voorbeeld van een examenopgave uit een 3F examen.

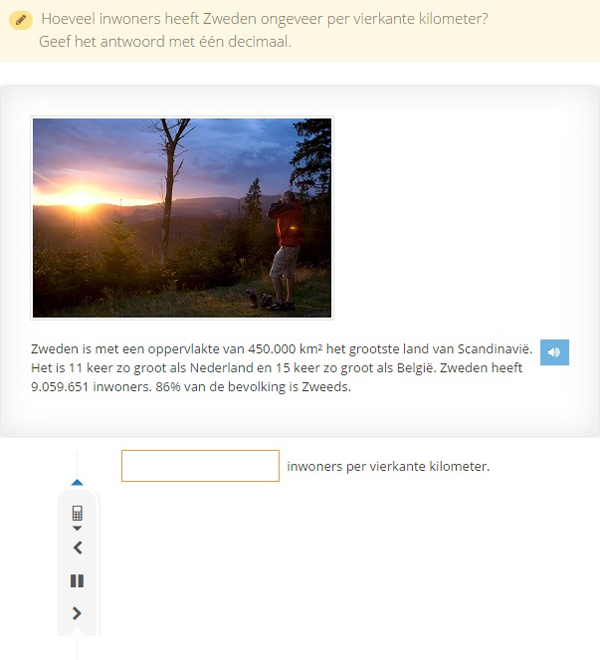
Bij het uitrekenen van een gemiddelde (in dit geval dus het gemiddelde aantal inwoners per vierkante kilometer) heb ik voldoende aan twee getallen: het totaal aantal inwoners, en de totale oppervlakte in vierkante kilometers. Kwestie van even delen, en het antwoord is daar. Ik moet het hier afronden op één decimaal, wat ergens een beetje raar is omdat 0,3 inwoner natuurlijk iets is wat ik in het dagelijks leven niet vaak zal tegen komen, maar daar kan ik nog wel langs heen kijken.

Het gaat nu uiteraard meer even om de toevoegingen in de tekst. ‘Het is 11 keer zo groot als Nederland en 15 keer zo groot als België.’ Uit ervaring kan ik inmiddels vertellen dat dit soort toevoegingen dermate veel impact heeft op de lezer, dat het mijns inziens veel te veel afleidt van wat ik zelf in een som als deze getoetst wil hebben; het kunnen berekenen van een gemiddelde. ‘86% van de bevolking is Zweeds.’ En we mikken er ook nog even een percentage bij in de tekst, want dat doet het ook altijd leuk. Ik ben best in staat om deze gegevens te nemen voor wat ze zijn: afleidingsmanoeuvres, niets meer en niets minder. Maar ik kan intussen ook vertellen dat zowel mijn leerlingen als mijn collega’s zich ernstig laten afleiden en amper nog in staat zijn om het juiste antwoord op deze som te geven.

En dan vraag ik me dus af: ben ik rekenen aan het toetsen, of begrijpend lezen? Schiet zo’n opgave niet een beetje voorbij aan het doel van het rekenexamen? U mag het zeggen.

(Quote is gehaald uit een adviesbrief van het Steunpunt Taal en Rekenen MBO, aan de minister van onderwijs; de examenopgave is er één van uitgever Deviant, gevonden in een 3F oefenexamen uit de digitale leeromgeving Studiemeter.)