Wat was er nou toch is met die goeie ouwe staartdeling? Die werkte toch altijd gewoon prima? Waarom snap ik nu niet meer hoe ze tegenwoordig een deelsom op moeten lossen?
Komen deze vragen je enigszins bekend voor? Het valt allemaal wel mee hoor. De staartdeling is er ook gewoon nog steeds (ze noteren ‘m ietsje anders – handiger zelfs – maar het is nog steeds een prima manier van oplossen), maar er was behoefte aan een manier die wat minder strak volgens een bepaald stramien moest, een manier die wat flexibiliteit bood.
Die manier doet de ronde onder diverse noemers; de ‘haakdeling’ heet ‘ie in het boek dat ik momenteel op school gebruik, dus die naam houd ik voor nu even aan.
Laat ik beginnen met nog even kijken wat een deelsom precies betekent.
3.456 : 72 =
In feite staat hier de vraag: hoe vaak past 72 in 3.456? Vanuit dat principe is de ‘nieuwe’ deelmethode bedacht. Een leerling zou in staat moeten zijn te bedenken dat het wel een keer moet passen. Het is de bedoeling dat je die één maal 72 van het totaal 3.456 af haalt, om dan te zien wat je over houdt, en je weer af te vragen hoe vaak 72 daar in past.
Op papier ziet het er dan (min of meer) zo uit: 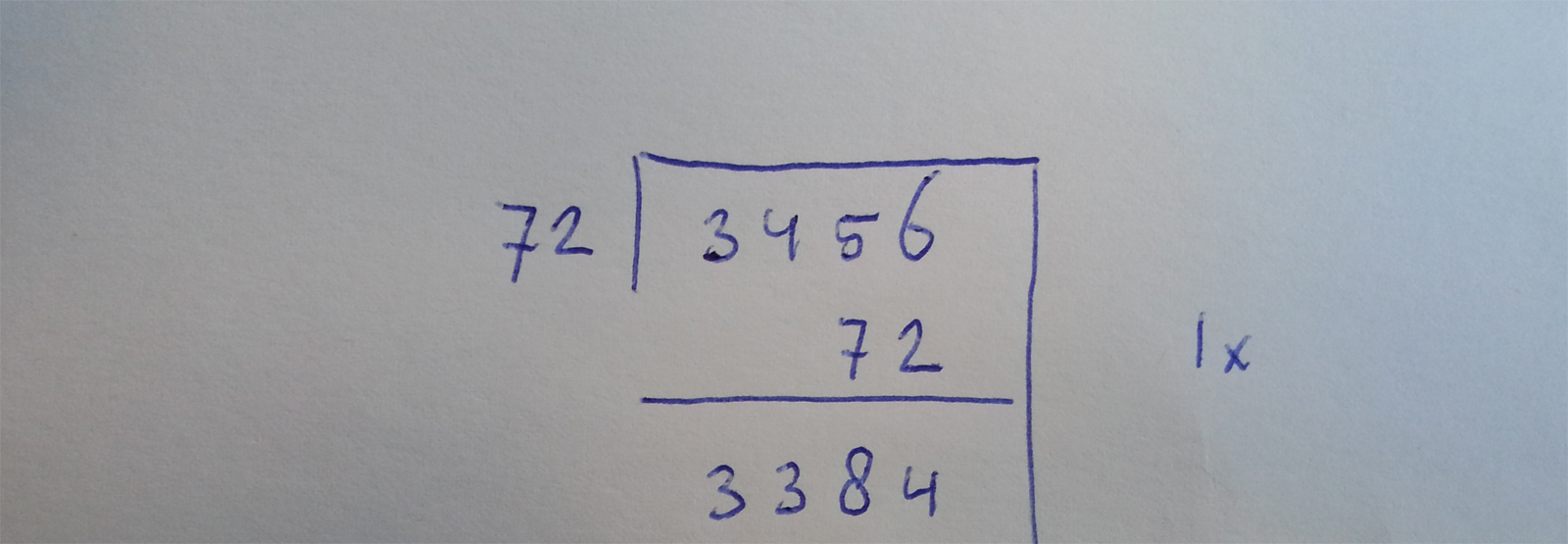
We hebben nu nog 3384 over. De vraag blijft; hoe vaak past daar nog 72 in? We kunnen veilig concluderen dat het nog wel een keertje past. Dit halen we dan ook weer van het overgebleven totaal af. Op papier hebben we dan dit: 
Je begint nu vast door te krijgen dat het zo nog wel even kan gaan duren. De meeste van mijn studenten gelukkig ook. We kunnen de stappen ook wat groter maken. Laten we bijvoorbeeld nu eens 10 x 72 in één keer er af halen, dan gaat het wat sneller… 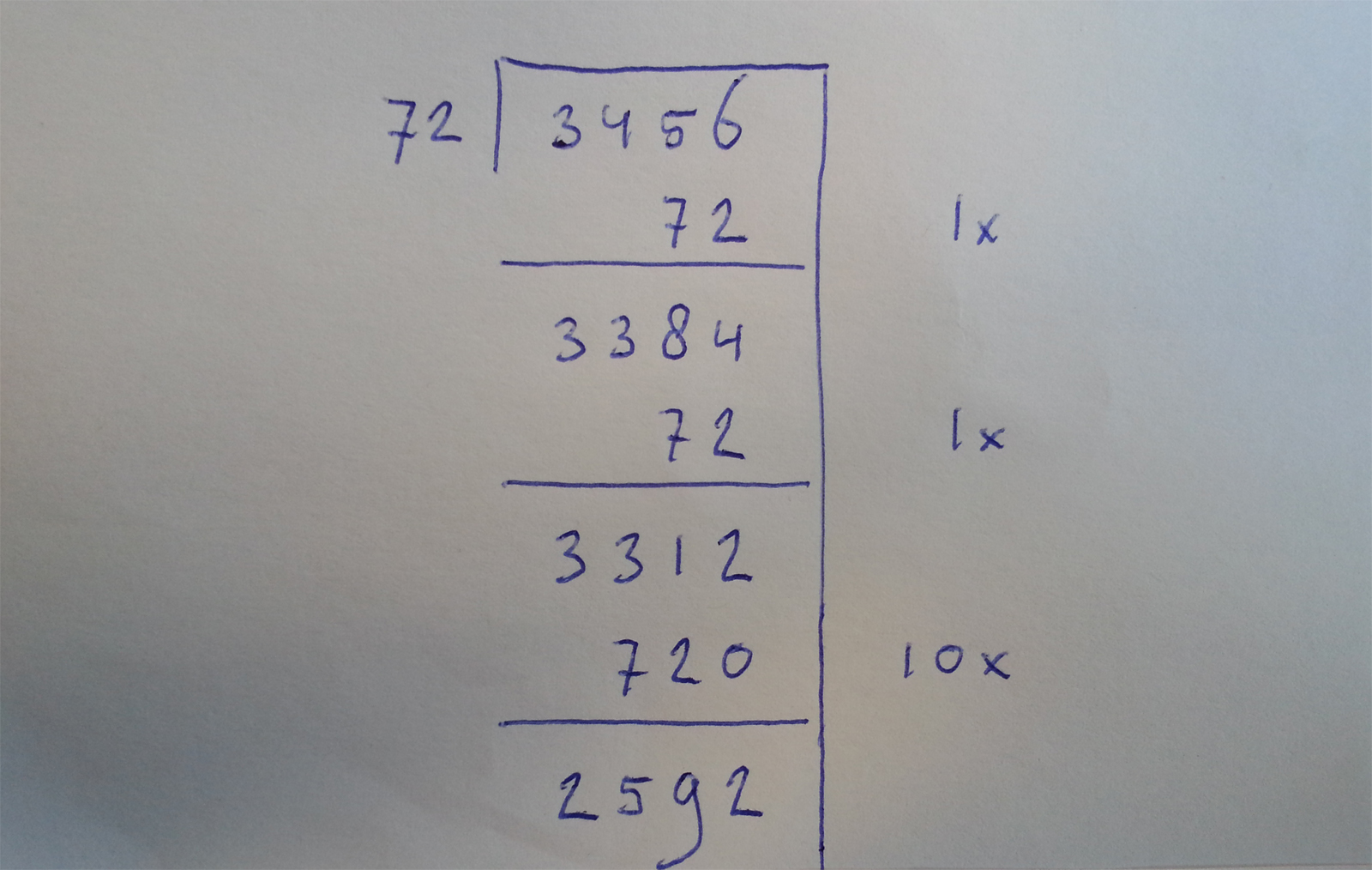
Dat scheelt al wat meer. We zouden op deze voet door kunnen gaan (sommige leerlingen doen dit dan ook, en dat is dus prima!), maar voor de wat stoerdere rekenaars onder ons kunnen we de stap nog wat vergroten; we halen er nu 20 x 72 af. Zo ziet onze som er uit:
Die laatste stap kunnen we niet meer herhalen; daar hebben we nu te weinig voor over. We kunnen wel één stap terug zetten, en en nogmaals 10 x 72 af halen. Daarna houdt ook die mogelijkheid op. Ik heb de som zelf nu af gemaakt door ook nog een keer 5 x 72 van het overgebleven totaal af te halen. Mijn overgebleven totaal wordt daardoor 72. Dan lukt het tenslotte nog één keer. Als het overgebleven totaal van de som uiteindelijk op 0 uit komt (bij deze som lukt dat; anders zouden we het nu hebben over delen met rest bijvoorbeeld – daarover later meer), tellen we hoe vaak we in totaal het getal 72 van het getal 3456 af hebben gehaald (1 + 1 + 10 + 20 + 10 + 5 + 1 = 48), en daar verschijnt het antwoord: 48.
Trouwe ‘fans’ van de staartdeling vinden dit misschien omslachtig, maar geloof me als ik zeg dat veel van mijn leerlingen erg gebaat zijn bij deze manier, die ze wat flexibiliteit biedt en ze in de gelegenheid stelt om zelf de controle over de som te houden.
Hopelijk geeft dit artikel een klein beetje inzage in wat je als ouder/begeleider misschien ooit eens voorbij hebt zien komen in een rekenschrift, en kun je, waar mogelijk, nog een beetje hulp bieden bij de uitleg.
In een toekomstig artikel zal ik de ‘nieuwe vorm’ van de goeie, ouwe staartdeling aan de orde stellen. Tot die tijd; oefen eens met de ‘haakdeling’, en zie of je jezelf er handiger in kunt maken.
