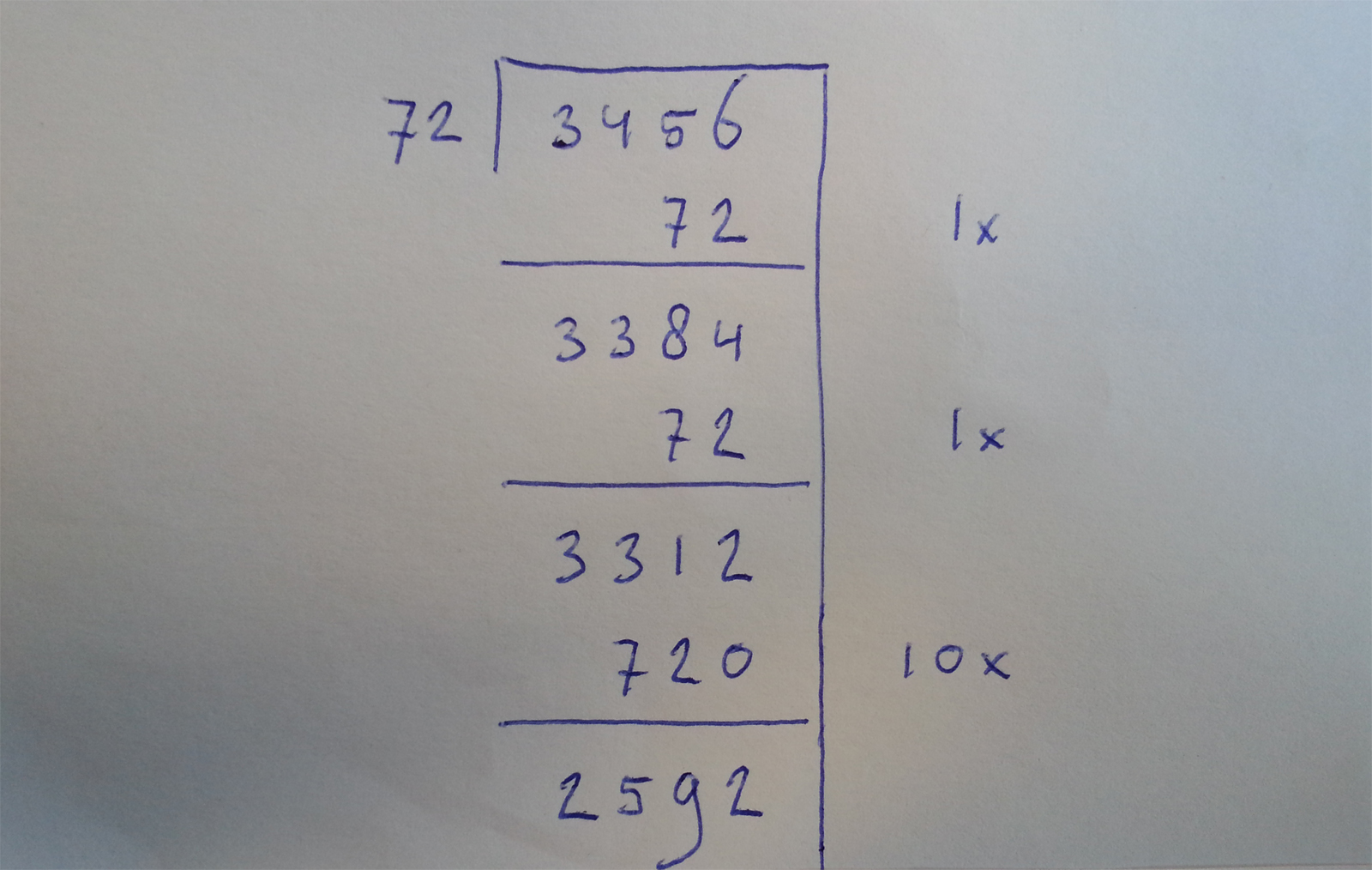
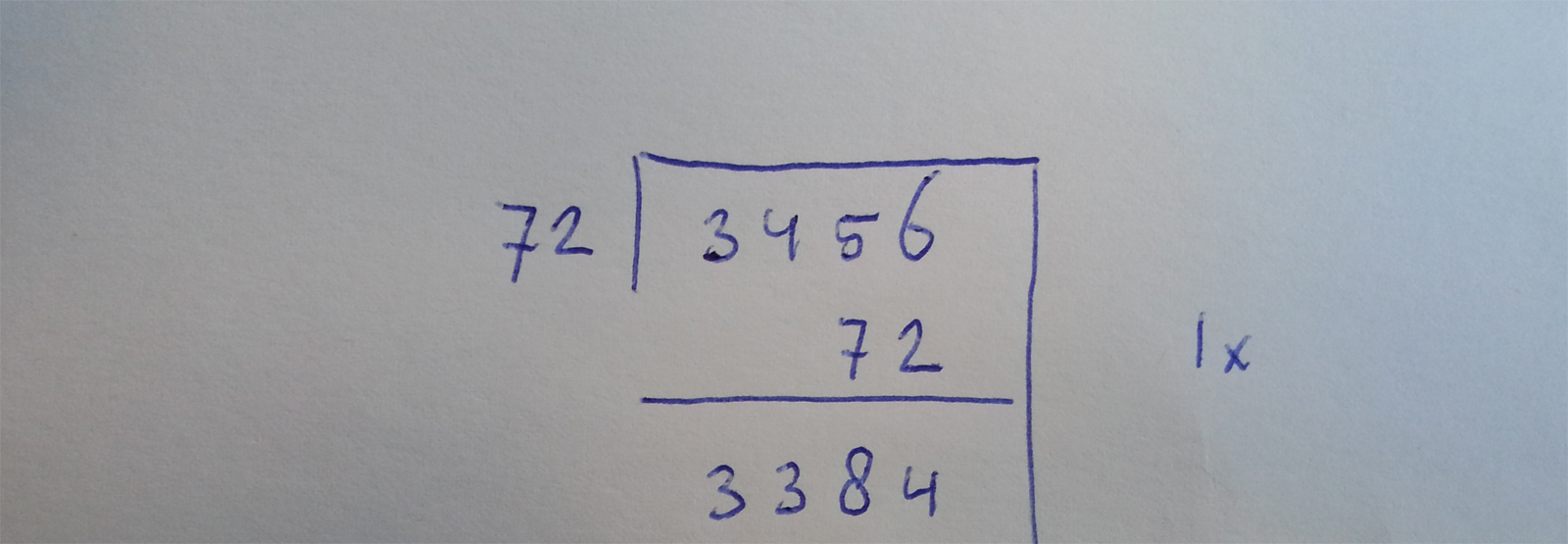Ik lees net een bericht (op Facebook, gelinkt vanaf AD.nl) met de titel “Perfecte score voor eerstejaars studenten Marnix Academie”.

Ik mag natuurlijk graag meteen denken dat daar vast een paar van mijn oud-studenten tussen zitten, want het gaat in dit artikel over de toelatingstoets voor het vak rekenen. Goed nieuws dus. Het is, bij mijn weten, altijd een van de grootste struikelblokken geweest bij het toegelaten worden tot de PABO. En het feit dat ALLE eerstejaars studenten op de Marnix Academie de toets gehaald hebben, stemt mij wel enigszins positief.

Ik mis wel wat details in het artikel, dus ik vul even in: ‘moeten deze landelijk vastgestelde toets maken in hun eerste jaar’ betekent wellicht dat studenten er een aantal pogingen aan mogen wagen, en dat er in het eerste jaar flink bijgespijkerd moet worden in sommige gevallen (waar er bij de laatste poging nog een flink aantal studenten zichzelf voorziet van een plekje in het tweede jaar), maar laat ik de boel nou niet bagatelliseren en gewoon blij zijn met dit resultaat!

Waarom dit artikel mij specifiek opviel? Ik ben een oud-student van de Marnix Academie. En ik haalde de rekentoets (eerste poging aan het begin van de opleiding) dus gewoonweg NIET. En ik heb enorm veel gehad aan de lessen van een zekere rekendocent daar op de Marnix Academie (Paul Stam, in die tijd; geen idee of de beste man er nog steeds werkt) die voor mij de eerste rekendocent was die met geduld, flexibiliteit en doorzettingsvermogen (had ik ‘geduld’ al genoemd?) de stof uitgelegd heeft weten te krijgen. Mijn interesse in het vak rekenen is toen pas gekomen.

Ik wil maar zeggen: het is dus prima mogelijk om een hele club eerstejaars studenten voldoende onderlegd te krijgen voor het vak rekenen om de PABO toelatingstoets te halen (misschien wil je zelf de uitdaging eens aan gaan?). Mijn stille hoop is nu, dat al deze studenten, NAAST het feit dat ze het vak zelf voldoende beheersen, ook energie willen steken in het vermogen om deze stof uit te kunnen leggen aan de kinderen die ze straks in hun klas hebben (geloof mij nu maar; dat is een heel andere vaardigheid!). Jullie maken namelijk het verschil. Op de basisschool al. Veel van mijn studenten hebben een ‘rekentrauma’ opgelopen, juist op de basisschool. Aan jullie de taak om er voor te zorgen dat ik, over een jaar of zestien, terug hoor van mijn studenten dat ze het vak rekenen hebben geleerd van een geduldige, flexibele leerkracht op de basisschool…

Gefeliciteerd met dit mooie resultaat!

Ik kwam vandaag een artikel tegen. Hier is een link. Het zal je wellicht niet verbazen dat ik hier ook een mening over heb.

Een quote uit het artikel luidt: “Bosman denkt dat het ook voor mensen met dyscalculie helpt om veel te oefenen. Ze liet vijftig leerlingen zes weken lang intensief trainen en volgens haar ging het niveau van de leerlingen gemiddeld met anderhalf jaar vooruit.”

Ik ben het hier intussen wel mee eens. Als ik een leerling tegen kom met de wil om beter te worden in het vak rekenen (die zijn, helaas, nog altijd vrij zeldzaam…), en ik bied ze enerzijds wat extra tijd voor uitleg en oefenen, en anderzijds zorgt zo’n leerling er zelf ook voor dat er wat extra tijd in het leren en oefenen van lesstof gaat zitten, dan verbetert eigenlijk in 100% van de gevallen het resultaat. Echt.

Zorg voor voldoende aandacht bij leerlingen die een achterstand dreigen op te lopen, en je ondervangt daarmee het grootste deel van de problematiek.

Het woord in dit artikel wat me het meest aansprak is ‘slecht’ onderwijs. Kun je van een gemiddelde basisschool leerkracht verwachten dat deze de extra tijd neemt om leerlingen extra uitleg te geven? Ja, verwachten kun je dat zeker. Maar is het ook reëel? Dat vraag ik mij nog steeds af. Ik weet, ook uit ervaring, wat er van je gevraagd wordt als leerkracht, en dan snap ik best dat de tijd die er voor nodig is om iemand extra aandacht te geven gewoonweg niet beschikbaar is. En lang niet alle scholen hebben bijvoorbeeld een RT-er in dienst die kan helpen met het bieden van de benodigde extra hulp.

Stof tot nadenken dus, want er wordt ECHT te makkelijk en te snel geroepen dat iemand dyscalculie / dyslexie heeft.

De rekentoets is nog altijd een prestige-object voor staatssecretaris Sander Dekker. Adviezen om het anders te doen, legt hij naast zich neer.

Om goed te leren rekenen is het nodig dat leerlingen op de basisschool tafels stampen, breuken oefenen en staartdelingen maken. Tot vervelens toe herhalen en automatiseren. Staatssecretaris Dekker kiest een andere route. Hij zet vol in op wat inmiddels zijn prestigeproject is geworden: de rekentoets. Nou ja, rekentoets? Het zijn vooral verhaaltjessommen, ingewikkelde plaatjes en instinkvragen die digitaal en met meerkeuzevragen worden afgenomen. En voor wie denkt dat de rekenvaardigheid van scholieren wordt getest door uit het hoofd te rekenen komt bedrogen uit. Bij verreweg de meeste vragen mag een rekenmachine worden gebruikt, dus uit het hoofd leren rekenen is er vaak niet bij.

Nee, het rekenen in de rekentoets moet vooral ‘leuk’ zijn en ‘toepasbaar’. Dat als gevolg hiervan zelfs de kampioene van de Wiskunde Olympiade, het beste wiskundemeisje ter wereld, niet minder dan zeven fouten maakte in haar ‘reken’toets zegt eigenlijk alles.

Natuurlijk is het best handig om op een landkaart aan te kunnen wijzen in welke plaats het welke temperatuur is. Maar met rekenen heeft dat niets te maken. En in spiegelbeeld klok kunnen kijken, om de juiste tijd in een meerkeuzevraag aan te klikken is vermakelijk, maar ik zou niet willen dat leerlingen omwille van een fout antwoord op zo’n vraag hun diploma mislopen.

Het CDA heeft staatssecretaris Dekker in een aangenomen motie gevraagd om met de vereniging van wiskundeleraren (NVvW) te overleggen hoe de rekenvaardigheid en het rekenonderwijs verbeterd kan worden en hoe dat het beste getoetst kan worden. Maar van open en reëel overleg is geen sprake geweest. De NVvW stelt onomwonden: ‘Het is zinloos om nog langer geld, tijd en energie te steken in het werken met de huidige digita le rekentoets. Niet alleen is het een ver keerd middel om de reken vaardig heid op peil te brengen, maar boven dien blijven er klach ten over de inhoud, de beoorde ling, het geheime karak ter, de digita le afname en de positie van de toets in de slaag-zakregeling.’ Klare taal van de rekenen- en wiskundeprofessionals.

Staatssecretaris Dekker spreekt warme woorden over het belang dat hij hecht aan de betrokkenheid van deze beroepsvereniging, maar gaat vervolgens volstrekt zijn eigen weg. Zonder overleg en zonder draagvlak.

Dit jaar vielen in het vwo al de eerste slachtoffers van de rekentoets, waar de toets meetelde voor het examen. Volgend schooljaar telt deze toets zelfs als kernvak mee op het vwo. Dat betekent dat één enkele rekentoets net zo zwaar weegt als zes jaar ploeteren op wiskunde, Engels of Nederlands.

Maar ook in de andere onderwijssoorten loopt de spanning op. De rekentoets is daar ook verplicht, maar telt nog niet mee voor het examen. De uitslagen bleken ondanks tal van kunstmatige ingrepen dramatisch. Ruim een derde van de vmbo’ers op de basisberoepsgerichte en kaderberoepsgerichte leerweg, 40 procent van de havisten en meer dan de helft van de mbo’ers haalt geen voldoende voor de rekentoets. Als deze rekentoets ook voor hen zou meetellen voor het examen, wat de staatssecretaris wil, is de schade niet te overzien.

Een goede rekenvaardigheid is van groot belang. En dus moeten we volop inzetten op goed rekenonderwijs. Maar het lijkt deze staatssecretaris niet te gaan om het rekenonderwijs, maar vooral om zijn prestigeproject, de rekentoets. En daar moeten we zo snel mogelijk van af.

Uit: nederands dagblad
16 november 2016, 03:00
Michel Rog • Tweede Kamerlid voor het CDA

Ook nog gevonden: een flyer voor studenten over het rekenexamen. Ik zou een slechte docent zijn als ik deze niet even linkte op mijn site.

En ja, ik zal ‘m ook meenemen naar de les, jongens en meisjes. Dan is het allemaal maar weer even duidelijk.

De Flyer.

Nou, het heeft even geduurd, maar daar zijn we dan weer. Een van de redenen van de lange stilte was het feit dat ik op rekenvlak even druk ben geweest met wat anders (resultaat daarvan volgt spoedig!), en een andere reden was de ontstane onduidelijkheid over het wel of niet meetellen van het rekenexamen op het MBO (waar ik dus werk).

Inmiddels is er meer duidelijk. Of niet. Het is wel een gegeven dat het examen ‘voorlopig’ niet meetelt op het MBO. Wanneer dan wel? Dat is niet bekend. Ik zou kunnen gissen, maar dat doe ik niet. In plaats daar van quote ik een tekst van het steunpunt, en mag je je eigen conclusie trekken. Het wachten is, blijkbaar, op het VO…

Rekenexamen mbo telt nog niet mee
Alle studenten in het middelbaar beroepsonderwijs maken een rekenexamen zoals eerder bepaald. Dat betekent in mbo-4 vanaf dit studiejaar en in de entreeopleiding, mbo-2 en mbo-3 met ingang van het studiejaar 2016-2017. Het resultaat van het rekenexamen telt de komende jaren nog niet mee voor het behalen van een diploma, maar wordt wel vermeld op de resultatenlijst bij het diploma.
Voor mbo-studenten telt het rekenexamen pas mee voor diplomering zodra de resultaten van de rekentoets in het voortgezet onderwijs voor alle leerlingen mee hebben geteld voor het behalen van het diploma. Dit zal voor het mbo ongeveer vier jaar zijn na het voor de eerste keer meetellen van de resultaten in het gehele vmbo en havo.

Langs de lengteschaal heet alles gewoon zoals het er staat (bijvoorbeeld “drie decameter”) – deze gebruik je om bijvoorbeeld een omtrek mee te berekenen, waarbij we ‘langs de lijnen’ lopen, en alle gemeten waarden bij elkaar optellen.

Bij de oppervlakteschaal heet alles ‘vierkant’ (bijvoorbeeld “zes vierkante meter”). De ‘2’ achter de afkortingen is een hint voor het aantal kommaplaatsen dat je moet opschuiven per stap, en komt tot stand door het vermenigvuldigen van een lengte met een breedte (2 ‘dimensies’). De ‘are’ en de ‘hectare’ worden vaak gebruikt in plaats van de termen ‘vierkante decameter’ en ‘vierkante hectometer’, maar in feite betekenen ze dus precies hetzelfde; handig om te weten bij het omrekenen!

Bij de inhoudsschaal heet alles ‘kubieke’ (bijvoorbeeld “zeven kubieke decimeter”) – dit komt van het woord ‘kubus’, en we gebruiken het om een inhoud te berekenen. De ‘3’ achter de afkortingen is een hint voor het aantal kommaplaatsen dat je moet opschuiven per stap, en komt tot stand door het vermenigvuldigen van een lengte met een breedte en een hoogte ( 3 ‘dimensies’).

De literschaal is ook een schaal voor inhoud, alleen schuif je op deze schaal slechts één kommaplaats op per stap (vergelijk ook eens de literschaal met de ‘kubieke’ schaal; je kunt daarop aflezen dat op beide schalen tussen een milliliter en een liter 3 kommaplaatsen zitten!). De inhoud van een kofferbak van een auto wordt bijvoorbeeld uitgedrukt in ‘liters’. Deze inhoudsschaal stop ook bij de ‘liter’ – we hebben het nooit over ‘decaliter’, ‘hectoliter’ en ‘kiloliter’, maar op de schaal bestaan ze wel.

De gewichtsschaal gebruik je (maar dat had je vast al geraden) bij het omrekenen van gewicht. Merk op dat er ook in deze schaal zeven stappen zijn, maar dat we er maar drie gebruiken. Die niet gebruikte tussenstappen verklaren namelijk wel waarom er tussen de ‘gram’ en de ‘kilogram’ drie kommaplaatsen zitten! Een ’ton’ tenslotte, is een term die we gebruiken voor ‘duizend (1000) kilogram’. Even opgelet: we gebruiken het woord ’ton’ ook bij geld, maar dan hebben we het over honderdduizend (100.000).

Net gevonden op het internet:

Het Landelijk Aktie Komitee Scholieren (LAKS) liet vijf Kamerleden onverwachts de rekentoets maken. De uitslag was opvallend: alle politici zakten.

Het volledige artikel, en de toets die de kamerleden hebben gemaakt, kun je hier vinden.

Wordt vervolgd…

Wat was er nou toch is met die goeie ouwe staartdeling? Die werkte toch altijd gewoon prima? Waarom snap ik nu niet meer hoe ze tegenwoordig een deelsom op moeten lossen?

Komen deze vragen je enigszins bekend voor? Het valt allemaal wel mee hoor. De staartdeling is er ook gewoon nog steeds (ze noteren ‘m ietsje anders – handiger zelfs – maar het is nog steeds een prima manier van oplossen), maar er was behoefte aan een manier die wat minder strak volgens een bepaald stramien moest, een manier die wat flexibiliteit bood.

Die manier doet de ronde onder diverse noemers; de ‘haakdeling’ heet ‘ie in het boek dat ik momenteel op school gebruik, dus die naam houd ik voor nu even aan.

Laat ik beginnen met nog even kijken wat een deelsom precies betekent.

3.456 : 72 =

In feite staat hier de vraag: hoe vaak past 72 in 3.456? Vanuit dat principe is de ‘nieuwe’ deelmethode bedacht. Een leerling zou in staat moeten zijn te bedenken dat het wel een keer moet passen. Het is de bedoeling dat je die één maal 72 van het totaal 3.456 af haalt, om dan te zien wat je over houdt, en je weer af te vragen hoe vaak 72 daar in past.

Op papier ziet het er dan (min of meer) zo uit: 

We hebben nu nog 3384 over. De vraag blijft; hoe vaak past daar nog 72 in? We kunnen veilig concluderen dat het nog wel een keertje past. Dit halen we dan ook weer van het overgebleven totaal af. Op papier hebben we dan dit: 

Je begint nu vast door te krijgen dat het zo nog wel even kan gaan duren. De meeste van mijn studenten gelukkig ook. We kunnen de stappen ook wat groter maken. Laten we bijvoorbeeld nu eens 10 x 72 in één keer er af halen, dan gaat het wat sneller… 

Dat scheelt al wat meer. We zouden op deze voet door kunnen gaan (sommige leerlingen doen dit dan ook, en dat is dus prima!), maar voor de wat stoerdere rekenaars onder ons kunnen we de stap nog wat vergroten; we halen er nu 20 x 72 af. Zo ziet onze som er uit:

Die laatste stap kunnen we niet meer herhalen; daar hebben we nu te weinig voor over. We kunnen wel één stap terug zetten, en en nogmaals 10 x 72 af halen. Daarna houdt ook die mogelijkheid op. Ik heb de som zelf nu af gemaakt door ook nog een keer 5 x 72 van het overgebleven totaal af te halen. Mijn overgebleven totaal wordt daardoor 72. Dan lukt het tenslotte nog één keer. Als het overgebleven totaal van de som uiteindelijk op 0 uit komt (bij deze som lukt dat; anders zouden we het nu hebben over delen met rest bijvoorbeeld – daarover later meer), tellen we hoe vaak we in totaal het getal 72 van het getal 3456 af hebben gehaald (1 + 1 + 10 + 20 + 10 + 5 + 1 = 48), en daar verschijnt het antwoord: 48.

Trouwe ‘fans’ van de staartdeling vinden dit misschien omslachtig, maar geloof me als ik zeg dat veel van mijn leerlingen erg gebaat zijn bij deze manier, die ze wat flexibiliteit biedt en ze in de gelegenheid stelt om zelf de controle over de som te houden.

Hopelijk geeft dit artikel een klein beetje inzage in wat je als ouder/begeleider misschien ooit eens voorbij hebt zien komen in een rekenschrift, en kun je, waar mogelijk, nog een beetje hulp bieden bij de uitleg.

In een toekomstig artikel zal ik de ‘nieuwe vorm’ van de goeie, ouwe staartdeling aan de orde stellen. Tot die tijd; oefen eens met de ‘haakdeling’, en zie of je jezelf er handiger in kunt maken.

6 : 3 x 2 = 1

Beste lezer, het zal je misschien ontgaan zijn, maar ergens in het voorbij gaan van de jaren, hebben wij een alom geliefde, zeer behulpzame, vriend verloren. Één die ons door vele moeilijke tijden heeft geholpen, die ons een uitweg bood als we die zelf niet meer zagen. Één die ons aan de hand nam, en ons keer op keer de oplossing voor een probleem liet zien.

Het doet me dan ook zeer om je te moeten vertellen dat Meneer Van Dalen niet meer op antwoord wacht; hij heeft zijn antwoord gekregen, en is verder gegaan met een ongetwijfeld hoger niveau van bestaan. In andere woorden: de rekenregel ‘Meneer Van Dalen Wacht Op Antwoord’ werkt niet meer!

Even opfrissen; het betreffende zinnetje was een ezelsbrug die ons vertelde in welke volgorde rekenkundige bewerkingen moesten plaatsvinden in een som waar meerdere bewerkingen achter elkaar stonden. ‘M’ staat voor Machtsverheffen, ‘V’ voor Vermenigvuldigen, ‘D’ voor Delen, ‘W’ voor worteltrekken, ‘O’ voor Optellen en ‘A’ voor Aftrekken. Dat toegepast op de som bovenaan deze tekst betekent dat we eerst het stuk 3 x 2 moeten doen (vermenigvuldigen komt, volgens Meneer van Dalen immers vóór delen). De som wordt dan vervolgens 6 : 6 , en ik denk dat we het allemaal eens zijn dat het antwoord daarop 1 is.

Helaas, de som 6 : 3 x 2 heeft vandaag de dag een andere uitkomst. Laat mij je dat uitleggen.

Ergens rond de millenniumwissel heeft men de oude rekenregel losgelaten, en een nieuwe aangenomen. Mijn Google-Fu is niet krachtig genoeg om precies te kunnen achterhalen wanneer dit was, maar de reden, zo heb ik mij laten vertellen, is dat bleek dat wij met onze regel afweken van wat men op de rest van de planeet deed. De conclusie dat dat niet zo verstandig is is uiteraard snel gemaakt. Dus aanpassen aan de rest, zodat het antwoord op elke som gelijk is, waar ter wereld je je ook bevindt. Logisch, toch?

Dan nu de ‘nieuwe’ regel. De nadruk ligt (nog steeds; dat gold bij Meneer Van Dalen ook, alleen leken we dat toentertijd gewoon voor lief te nemen) op dat alles wat tussen haakjes staat, eerst uitgerekend moet worden. Dat noemen we bij dezen dus regel 1.

1 . Haakjes eerst

Vervolgens komen de bewerkingen machtsverheffingen en worteltrekken. De volgorde van beiden maakt niet uit, omdat het elkaars tegengestelde berekeningen zijn, en dus wordt besloten, omdat we leren van links naar rechts te lezen, om de bewerkingen ook op volgorde van links naar rechts te doen. Puntje bij paaltje;  regel 2 luidt:

2. Machtsverheffingen & Worteltrekken

Nu komen vermenigvuldigen en delen aan de beurt. Ook voor deze bewerkingen geldt dat ze elkaars tegengestelde zijn, en dus ook hiervoor geldt nu dat de we bewerkingen van links naar rechts afhandelen. Door deze regel klopt het antwoord op de som bovenaan deze tekst ook niet meer, maar daarover zo meteen meer. Regel 3 ziet er dan als volgt uit:

3. Vermenigvuldigen & Delen

Tenslotte hebben we nog optellen en aftrekken (waarbij ik graag een keer noem dat hier in de klassen, de laatste term toch iedere keer weer een voorspelbare reactie uit mijn diverse klassen komt – pubers!), die ook bij Meneer Van Dalen een beetje het ondergeschoven kindje waren. Andermaal geldt dat ook deze twee bewerkingen elkaars tegengestelde zijn, en dus van links naar rechts door de som afgehandeld moeten worden. En voilà, daar is regel 4:

4. Optellen & Aftrekken

Speciaal voor de mensen die moeite hebben met het loslaten van een ezelsbruggetje, zij die de houvast van een slim bedacht, eenvoudig te onthouden zinnetje, heb ik een aardigheidje. We zetten de vier regels even onder elkaar:

1. Haakjes
2. Machten & Wortels
3. Delen & Vermenigvuldigen
4. Optellen & Aftrekken

Ik heb de eerste letter van alle woorden vet gemaakt. Ik kies er voor om ze in deze volgorde te zetten, omdat anders mijn slimmigheidje niet werkt, maar ik daag je graag uit om zelf ook een ezelsbruggetje te verzinnen (en onthoud daarbij dat je, per regel, de volgorde van beide bewerkingen mag wisselen). Met de letters in de hierboven gekozen volgorde krijg je dus:

Haakjes – Machten – Wortels – Delen – Vermenigvuldigen – Optellen – Aftrekken

En daarmee kun je het volgende zinnetje maken:

Hoe Makkelijk Was De Volgorde Ook Alweer.

Alsjeblieft, je nieuwe ezelsbruggetje is daar. Simpel, nietwaar? Tenslotte nog even terug naar de som bovenaan de tekst.

Meneer Van Dalen ‘dwong’ ons nog eerst te vermenigvuldigen en daarna pas te delen. De nieuwe regel maakt beide bewerkingen gelijkwaardig, en dus van links naar rechts af te handelen. Het nieuwe antwoord komt dus tot stand door eerst 6 : 3 = 2 te doen, en daarna het overgebleven getal te vermenigvuldigen met 2.

6 : 3 x 2 = 4